Photo by Dan Cristian Pădureț on Unsplash
Behind the Scenes: A Deep Dive into the Frax Finance Algorithm
What is Frax Finance?
Frax Finance is the protocol around the $FRAX stablecoin, that's pegged in a 1:1 ratio to the US Dollar. There are two main components in the protocol:
Price Oracle
The Collateralization Mechanism
We'll cover both of them in this article, however, we won't cover the actual implementation of these components.
Price Oracle
The most important thing to understand is: $FRAX is a 'hybrid' stablecoin. That means it's partly collateralized, partly backed by the algorithm we'll discuss next. The second most important thing is: the Frax protocol has a governance token, $FXS that's not stable. This token will be burned and minted by the collateralization mechanism. Now, we understand the backbone of the protocol and the hybridness of $FRAX, let's discuss the actual price oracle.
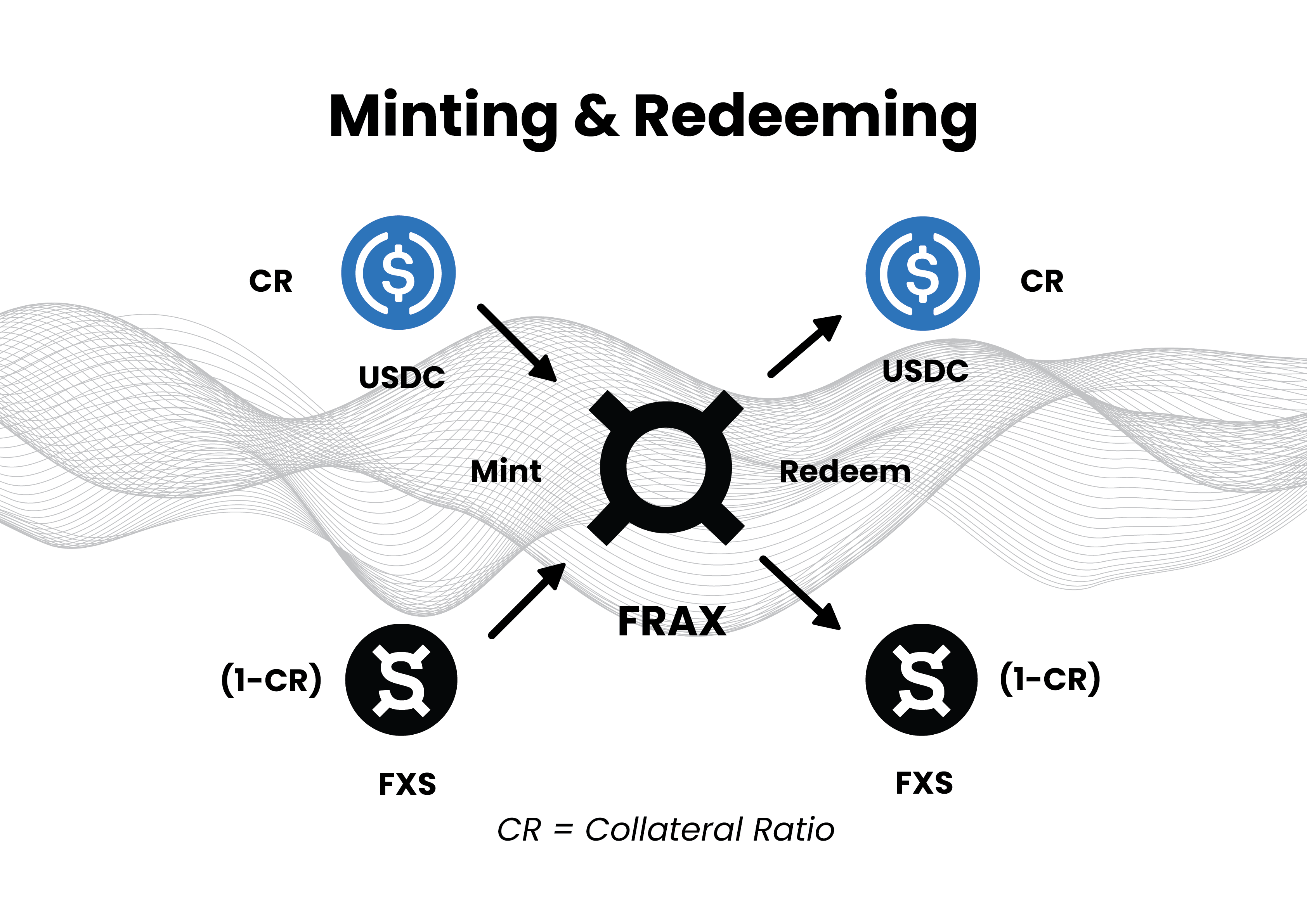
The hybridness means, if you want to mint one $FRAX, you'll need one $USD, but in the percentage of the collateralization. If this percentage is 100% you'll need, one dollar, for example in $DAI to mint one $FRAX. If it's 90%, you'll need 90 cents in $DAI, and 10 cents in $FXS which will be burned. This ratio is adjustable by the Frax DAO.
The redemption of your $FRAX works in a reversed order. If the percentage is 90%, you'll get $DAI worth 90 cents, and $FXS worth 10 cents minted to your address, and the redeemed $FRAX will get burned in the process.

This supply and demand curve illustrates, how the process of minting and redeeming helps to stabilize the price, meaning it'll be as close to one dollar as possible.
When the price of $FRAX is at its target level of $1 (represented by p0), the quantity of $FRAX in circulation is at its base level (represented by q0), this point is intersected by the CD0 curve. The CD1 curve's first intersection at p1 and q0 means an increase in the price of $FRAX - thanks to the increased demand - but an unchanged supply. In order to get the price back down, back to $1, new $FRAX must be minted, until the supply reaches q1, resulting in the price's drop back to p0.
But what about the squares? Good question. Since the market capitalization is calculated as the product of price and quantity, the market cap of $FRAX is at q0 is the blue square, at q1 is the blue square, plus the green square. The red square represents a potential increase in market cap, if the price increases, while the quantity of tokens in circulation, remains the same.
Note: the half-shaded portion of the green square represents the value of $FXS tokens that would be burned if the new quantity of $FRAX was minted at the collateral ratio of 66%.
The Collateralization Mechanism
Now comes the fun part: the actual collateralization algorithm, which can be divided into two parts:
Minting
Redeeming
We'll deal with a bit of algebra, but I will try to keep it as simple as possible.
Minting
An important thing to note: $FRAX is a fungible token, which means that one $FRAX is the same as another.
For the sake of simplicity, I changed the variable names, from the original documentation which I'll link below.
F is the units of newly minted $FRAX
Cr is the collateral ratio (0,9 = 90% is collateralized)
Cu is the units of collateral transferred to the system
Pc is the price of Cu in $USD
S is the units of $FXS burned
Ps is the price of S in $USD
$$F = Cu Pc + S Ps$$
This equation describes the relationship between the units of collateral (Cu), units of $FXS burned ($FXS price * $FXS units), and the units of $FRAX minted. But we have a problem: how do we know the amount of $FXS that should be burned (S) based on its price and the value of the collateral (Cu \ Pc*)?
Here is our answer:
$$(1 - Cr) Pc Cu = Cr Ps S$$
Now we need a bit of time to prove, this is true.
1. Isolate S because this is the only unknown
$$\frac{(1 - Cr) Pc Cu}{(Cr * Ps)} = S$$
Since (1 - Cr) and Cr are both constants, and Pc and Ps are also constants, we can say that (1 - Cr)*Pc\ Cu* and Cr * Ps are also constants. Therefore, S is a constant as well.
This means that the value of S is fixed and does not depend on any other variables, which demonstrates that (1 - Cr)*Pc *Cu = Cr \Ps* *S is a true statement. While doing this proof we also found a more straightforward and elegant way to calculate the unknown we need for our first equation!
Example No.1:
Minting $FRAX at a collateral ratio of 100% with 200 USDC ($1/USDC price). To be explicit, we can start by finding the $FXS needed to mint $FRAX (S).
$$\frac{(1 - 1) 1 200}{(1 * 1)} = S$$
In this example, it's very clear that S is 0, so in the first equation we only the price of the collateral (Pc) and the amount of the collateral (Cu) which we know will equal 200.
Example No.2:
Minting $FRAX at a collateral ratio of 80% with 120 $USDC ($1/USDC price) and an $FXS price of $2.
$$\frac{(1 - 0.8) 1 120}{(2 * 0.8)} = S$$
This will leave us with 15 $FXS needed to be burned.
$$F = 120 1 + 15 2$$
This 120+30=150, which means we'll get 150 $FRAX tokens.
Redeeming
The redeeming process can easily be described by rearranging the previous equations. This will be a bit simpler, because we need two values at the end, and we have two equations.
F is the units of $FRAX redeemed (burned)
Cr is the collateral ratio (0,9 = 90% is collateralized)
Cu is the units of collateral transferred to the user
Pc is the price of Cu in $USD
S is the units of $FXS minted to the user
Ps is the price of S in $USD
$$\frac{F * Cr}{Pc}=Cu$$
and
$$\frac{F*(1-Cr)}{Ps}=S$$
We won't prove these equations, since they're just the rearrangement of the previous two, but there'll be two examples:
Example No.3:
You have 100 units of $FRAX that you want to redeem. The current collateral ratio is 75% and the price of the collateral (in this case, $USDC) is $1.00. The price of $FXS is $3.50.
$$\frac{100 * 0.75}{1}= \frac{75}{1}=75$$
We'll get 75 $USDC worth $75. We're missing $25, but we haven't run our second equation, yet.
$$\frac{100*(1-0.75)}{3.50}=\frac{25}{3.5}≈7.1428$$
This isn't the roundest number ever, but 7.1428*3.5+75*1=99.9998 which is pretty close to 100. Our customer has only lost 0.0002% of his money (important to note: there's an adjustable mint/redeem fee, in the Frax protocol).
Example No.4:
Redeeming 120 $FRAX at a collateral ratio of 60% with an $FXS price of $2.25, and with a $USDC price of $1.02.
$$\frac{120 * 0.6}{1.02}= \frac{72}{1.02}≈70.588235$$
We know how much $USDC we'll get, let's calculate the $FXS.
$$\frac{120*(1-0.6)}{2.25}=\frac{48}{2.25}≈21.333$$
Okay, because 70.588235*1.02+21.333+2.25=119.9992497, we were only 0.0007503, which is roughly 0.000625%.
Thanks for reading! In the second part, I'll cover the Frax V2 algorithm which uses Algorithmic Market Operations Controllers (AMO), and how it improves upon the current collateralization mechanism.
This article is based on: